The Sine Cosine Project

 

An apparatus that calculates sines and cosines helps understanding the properties of these important functions.

Periodicity, Oscillation, Cycles

Phenomena that are periodic are all around us. Examples include sound waves, vibrating strings, light waves, ocean waves, ripples on the water, ripples on the sand, bouncing balls, pendulums, clocks, electronic oscillators, motors, blinking lights, orbiting planets, quasars, flapping wings, seasons, tornados, and rotating wheels. All of these can be described quantitively using the sine or cosine functions. Understanding these functions allows us to understanding and predict periodic effects.

Sine and Cosine

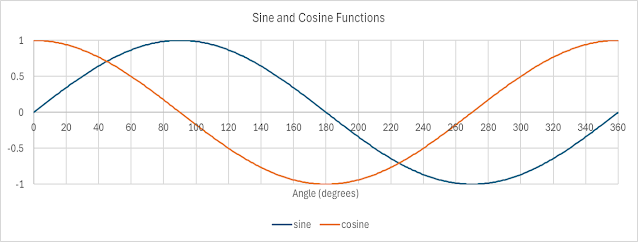
For any number $\alpha$, you can look on a graph like the one below to find a corresponding value for $\sin \alpha$ or $cos \alpha$. If $\alpha$ is an angle, measured in degrees, then this graph tells us that if $\alpha = 0^\circ$ then $\sin \alpha = 0$ and $\cos \alpha = 1$, or if $\alpha = 90^\circ$ then $\sin \alpha = 1$ and $\cos \alpha = 0$. But where do the sine and cosine values come from?

The Circle

A circle is a set of points all the same distance from a center point. If we place a circle on a grid with the horizontal axis labeled x and the vertical axis labeled y, we can locate any point on the circle by its distance from the center along x and its distance from the center along y. In the example below, for a circle of radius 1, the red point is located by going along x a distance 0.866, and along y by 0.5. The green point is at x = -0.866 and y = -0.5.

The Circle and Sine, Cosine

Another way to specify the location of a point on a circle is to go from the center along the horizontal axis a distance R = radius, then along the circle to an angle $\alpha$. In the case below, the red dot is on a circle of radius R = 1 and at an angle $\alpha =  30^\circ$, measured from the horizontal axis. When R = 1, the values of x and y for the point are related to $\alpha$ by $x = \cos \alpha$ and $y = \sin \alpha$. If we tabulate the x and y values for points on this circle for each angle, we can create a table for the sine and cosine of all angles.

The Apparatus

The goal is to make a machine that tells us the sine and cosine of any angle from 0° to 360°. A rotating wheel is a simple mechanism for this. Each revolution acts as a full cycle of periodic motion.

Note: The bearing wheel design and fabrication was by Hobby Machinist Keith

Mechanism:

The main wheel is made from ½” MDF, cut with a radius jig and router. Two horizontal cosine scales (linear from -1 to 1) are bolted to a ½” MDF base (blue). The sine scale (linear -1 to 1 vertical) is attached to two sets of aluminum wheels that roll in a ¼” wide U channel. The bottom wheels are spring loaded to maintain tension and wheel contact. As the large wheel is turned, a small pin anchored to the wheel edge (red) indicates the angle and contacts the sine scale, pushing it along the cosine rails. By keeping the pin in contact with the sine scale, the angle and its sine and cosine values are indicated. In the photo, the wheel is rotated to $30^\circ$ showing $\sin{(30^\circ)} = 0.50$ and $\cos{30^\circ} = 0.865$.

Scales used to print onto adhesive paper. Sizes were adjusted to fit the inner circle to the wheel diameter.

Exploring Sine and Cosine

Many of the basic properties of sine and cosine can be discovered using this apparatus. A few examples are given.

Relations between sine and cosine

Looking at the sine and cosine curves, we see that they are really the same shape, just shifted by 90°. If we use the machine (images below) to find sine and cosine for 30° and 60° (= 90° – 30°), we find that the values are just reversed: cos(30°) = sin(90° - 30°) and sin(30°) = cos(90° - 30°). In general, we find $\cos{(\alpha)} = \sin{(90° - \alpha)}$, and $\sin{(\alpha)} = \cos{(90° - \alpha)}$. We can also look at what happens if we add 90° to an angle. We find sin(60°) = -cos(90° + 60°), and cos(60°) = sin(90° + 60°). Also, sin(30°) = -cos(90° + 30°), and cos(30°) = sin(90° + 30°). In general, $\cos{(\alpha)} = \sin{(90° + \alpha)}$, and $\sin{(\alpha)} = - \cos{(90° + \alpha)}$. 

Changing the sign of an angle

If we change the sign of an angle, sine and cosine have a different response. An angle of $\alpha = -10°$ is the same as 360° - 10° = 350°. Moving the wheel on the apparatus from 10° to 350°, we see that the cosine value retains its positive sign (and its magnitude hardly changes from 1), but the sine values go from + to – symmetrically about 0°. From this we can conclude that $\sin{(-\alpha)} = - \sin{(\alpha)}$ and $\cos{(-\alpha)} = \cos{(\alpha)}$.

Sum of squares

Take the square of sin(30°) and add it to the square of cos(30°), using the values read from the wheel: $\cos^2(30°) + \sin^2(30°) = 0.865^2 + 0.5^2 = 0.998$, very close to 1.  The same is true for 60° and any other angle in the circle. In general, we find $\cos^2\alpha + \sin^2\alpha = 1$. This rule can be understood from Pythagoras Theorem: For a right triangle of sides x and y and diagonal (hypotenuse) R, the theorem states $x^2 + y^2 = R^2$. In our case R = 1, $x = \cos\alpha$ and $y = \sin\alpha$, which becomes $\cos^2\alpha + \sin^2\alpha = 1$. As a result, knowing the cosine allows us to calculate the sine and visa versa.

Approximations for small angles

If we measure $\sin\alpha$ for $\alpha$ near 0° and plot the results, we can see a very linear behavior, allowing us to approximate $\sin\alpha \approx 0.017 \alpha$, when $\alpha$ is measured in degrees. If we measure angles using radians ($\alpha_r$), where a full revolution gives us $\alpha_r = 2\pi$ radians we have the conversion $\alpha_r = \frac{2\pi}{360} \alpha = 0.017 \alpha$. The expression then becomes $\sin\alpha_r \approx \alpha_r$. For $\cos\alpha$, we find that it is close to 1 over this range, with a slight downturn.

Approximations for cosine near 90°

If we measure $\cos\alpha$ for $\alpha$ near 90° and plot the results vs. $90° - \alpha$, we again see a very linear behavior, allowing us to approximate $\cos\alpha \approx 90° - 0.017 \alpha$, when $\alpha$ is measured in degrees. In radians this expression becomes $\cos\alpha_r \approx \pi/2 - \alpha_r$. Similarly, we find $\sin\alpha \approx 1$ in this range. This is consistent with the earlier result that $\sin\alpha = \cos(90° - \alpha)$. 

The Inverse of Sine and Cosine

Often, we need to know what angle corresponds to a specific value of sine or cosine. If we know the y coordinate of a point on the circle is 0.5, what is the value of $\alpha$? Turning the wheel until $y = \sin\alpha$ shows 0.5 at the pin position, we find that $\alpha = 30°$ or $150°$. The corresponding x values are $x = \cos\alpha = + 0.865$ or $– 0.865$, so we also need to know x to fully determine the angle. 

This is called the inverse function, written as $\arccos(x) = \alpha, \arcsin(y) = \alpha$ or $cos^{-1}(x) = \alpha, sin^{-1}(y) = \alpha$.

Squaring of the Circle

A famous mathematical puzzle that once pre-occupied Leonardo da Vinci was to draw a square whose area was the same as that of a circle, using only a drawing compass and straight edge. It was proven in 1882 that this was not possible to do exactly. Using the sine-cosine wheel we approximate the angles of the points of intersection of the circle and square. The area of the circle whose radius R = 1 is $\pi R^2 = \pi$. A square of the same area must then have sides of length $\sqrt{\pi}$. When overlaid on the circle, the lines of the square then extend from -0.886 to +0.886, as shown in the graph below. To find the intersection angle $\alpha$, we use $\alpha \approx \arccos(0.885)$. Moving the wheel to the value of cosine $\approx 0.885$ shows that the angle $\alpha \approx 27.5°$. The next intersection is at $90° –\alpha \approx 62.5°$. Note that since the circle and square have the same area, the regions A and B must also be equal.